字典树(Trie)
1. 单级字典树
字典树最基础的应用——查找一个字符串是否在「字典」中出现过,也可以用来做最长前缀匹配。
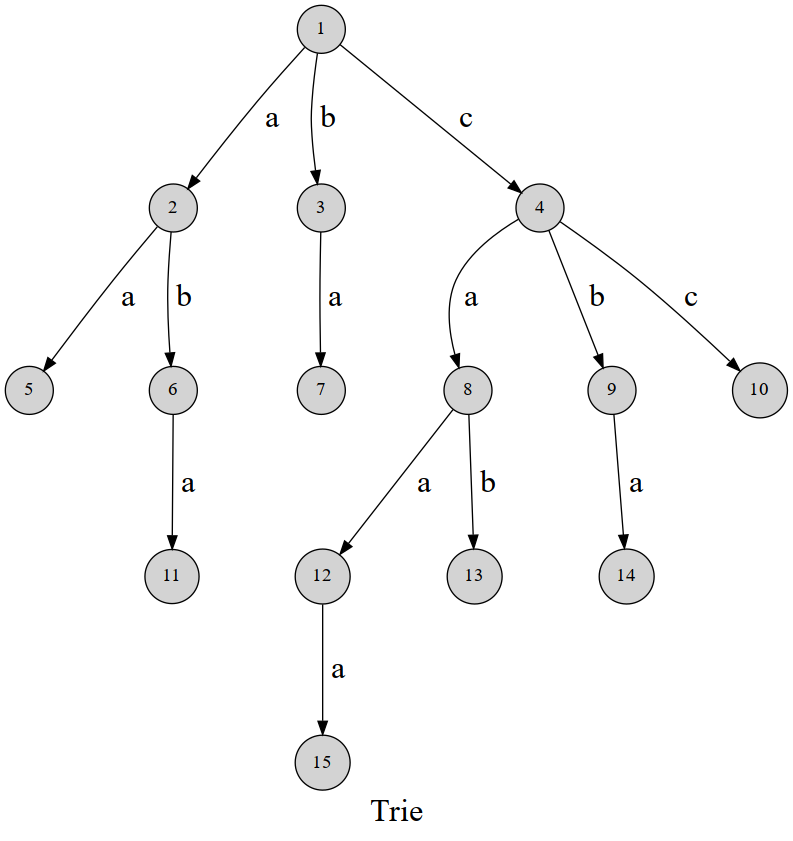
如下图,每个路径代表一个字母,每个节点存储以该节点结尾的字符串是否存在,构建如下的一个字典树。
1-4-8-12,且12节点记录值为true,则代表存在这样的路径的字符串,即存在caa字符串。
最长前缀匹配即,在字典树中一直往下中,直到到某个叶子节点的路径值与待匹配字符串不匹配,则从根节点到这个叶子结点的父节点的路径代表的字符串就是找到的满足最长前缀匹配的字符串。
1.1. 复杂度
1.1.1. 时间复杂度
构建字典树复杂度为o(n),n为元素数量
插入、删除、查找复杂度o(k),k为树的最大深度
1.1.2. 空间复杂度
字典树每个节点都需要用一个数组来存储子节点的指针,即便实际只有两三个子节点,但依然需要一个完整大小的数组。所以,字典树比较耗内存,空间复杂度较高。
如果构建一个二进制0-1字典树,存一个0101010101的二进制,需要10个路径,11个节点,每个节点需要一个二维数组,所占空间极大。例如,存一个4字节的ip地址,则需要2 + 4 + 8 + ... + 2^32个数组元素。
<span class="tag">#include</span> <iostream>
<span class="tag">#include</span> <unordered_map>
<span class="tag">#include</span> <string>
// Trie节点类
class TrieNode {
public:
std::unordered_map<char, TrieNode*> children; // 存储子节点
bool isEndOfWord; // 标记是否为单词结尾
TrieNode() : isEndOfWord(false) {} // 构造函数初始化isEndOfWord为false
};
// Trie树类
class Trie {
private:
TrieNode* root; // 根节点
public:
Trie() {
root = new TrieNode(); // 初始化根节点
}
// 插入单词
void insert(const std::string& word) {
TrieNode* node = root;
for (char c : word) {
if (node->children.find(c) == node->children.end()) {
node->children[c] = new TrieNode(); // 如果子节点不存在,则创建新节点
}
node = node->children[c]; // 移动到子节点
}
node->isEndOfWord = true; // 标记单词结尾
}
// 搜索单词
bool search(const std::string& word) {
TrieNode* node = root;
for (char c : word) {
if (node->children.find(c) == node->children.end()) {
return false; // 如果子节点不存在,则单词不存在
}
node = node->children[c]; // 移动到子节点
}
return node->isEndOfWord; // 返回是否为单词结尾
}
// 判断是否存在以prefix为前缀的单词
bool startsWith(const std::string& prefix) {
TrieNode* node = root;
for (char c : prefix) {
if (node->children.find(c) == node->children.end()) {
return false; // 如果子节点不存在,则前缀不存在
}
node = node->children[c]; // 移动到子节点
}
return true; // 前缀存在
}
};
int main() {
Trie trie;
trie.insert("hello"); // 插入单词"hello"
trie.insert("world"); // 插入单词"world"
std::cout << std::boolalpha;
std::cout << "Search 'hello': " << trie.search("hello") << std::endl; // 搜索单词"hello"
std::cout << "Search 'world': " << trie.search("world") << std::endl; // 搜索单词"world"
std::cout << "Search 'hell': " << trie.search("hell") << std::endl; // 搜索单词"hell"
std::cout << "Starts with 'wor': " << trie.startsWith("wor") << std::endl; // 判断是否存在以"wor"为前缀的单词
std::cout << "Starts with 'he': " << trie.startsWith("he") << std::endl; // 判断是否存在以"he"为前缀的单词
std::cout << "Starts with 'he': " << trie.startsWith("hw") << std::endl; // 判断是否存在以"hw"为前缀的单词
return 0;
}
1.2. 优化
1.2.1. 链表
使用链表来存储子节点。每个节点包含一个链表,链表中的每个元素是一个键值对,键表示字符,值表示对应的子节点。这样可以避免固定数组带来的空间浪费,尤其适用于字符集稀疏的情况
1.2.1.1. 查找效率较低
- 线性查找开销:链表存储子节点时,查找特定子节点需要遍历链表。在最坏情况下,若链表长度为 ,查找时间复杂度为 。例如,在一个处理字母字符集的字典树中,若某个节点的子节点通过链表存储,要查找字符 'z' 对应的子节点,可能需要遍历链表中的每个元素,直到找到 'z' 或者遍历完整个链表,这相较于使用数组直接通过索引访问子节点,效率明显更低。
- 增加查找时间:随着字典树规模增大和子节点数量增多,链表长度变长,查找特定子节点所需的时间也会相应增加,进而影响整个字典树的查找性能,尤其是在需要频繁进行查找操作的场景下,这种效率问题会更加突出。
1.2.1.2. 内存局部性差
- 非连续内存访问:链表的节点在内存中通常不是连续存储的,每个节点可能分布在内存的不同位置。当需要访问子节点时,由于内存的非连续性,会导致大量的内存随机访问,增加了缓存不命中的概率。例如,在现代计算机系统中,CPU 缓存通常会预取连续的内存数据以提高访问速度,而链表的非连续特性使得缓存预取策略难以发挥作用,从而降低了数据访问的效率。
- 影响性能:频繁的缓存不命中会使 CPU 等待数据从内存传输到缓存,增加了数据访问的延迟,进而影响字典树的整体性能。特别是在处理大规模数据时,内存局部性差带来的性能问题会更加显著。
1.2.1.3. 插入和删除操作复杂
- 插入操作:在链表中插入一个新的子节点,需要先遍历链表找到合适的插入位置,然后进行指针的调整,涉及多个步骤和指针操作。例如,若要将新节点插入到链表中间位置,需要先找到插入位置的前一个节点,然后修改前一个节点的指针指向新节点,再将新节点的指针指向原插入位置的节点,操作较为繁琐,时间复杂度为 。
- 删除操作:删除链表中的一个子节点同样需要遍历链表找到要删除的节点,然后修改前后节点的指针,以确保链表的连续性。若删除节点后链表为空,还需要额外处理父节点的指针。与数组直接通过索引删除元素相比,链表的删除操作更为复杂,也需要 的时间复杂度。
1.2.1.4. 不适合并行操作
- 链表结构限制:链表的线性结构使得其难以进行高效的并行操作。因为链表中的节点依赖于前一个节点的指针,在并行处理时,很难同时对多个节点进行操作,否则可能会破坏链表的结构和指针关系。
- 降低并行性能:在多核处理器环境下,无法充分利用多核的并行计算能力,这在需要处理大量数据和高并发的场景中,会成为性能瓶颈,限制了字典树在并行计算方面的应用。
1.2.2. 缩点优化
将末尾一些只有一个子节点的节点,可以进行合并,但是增加了编码的难度
( ) ()
/ \ / \
a s a siab
/ \ \ / \
b d i b drf
/ \ \ \ / \
c f r a c f
\ \
f b
2. 多级字典树
可以在多个字典树中查找所有满足条件的结果,第一个字典树查出来集合{A,C,F,G},则在第二个字典树进行查找的时候需要添加额外条件,即匹配结果需要额外满足在第一个字典树的集合{A,C,F,G}中。